Fallacy Solutions

Proof #1

The illegal step is in going from the fourth to the fifth line

since a and b are equal, a - b equals zero.  To get rid of them from the equation, they have to divide out, and dividing by zero is a no no.

Proof #2

Now that you know the answer to the first one, go back and try the second one.

Did you do it?

The reason is the same as in Proof #1.  You cannot divide by zero.

Proof #3

Here's one with numbers that doesn't involve division by zero.  The error is in going from the fifth to the sixth step

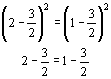
The right side of the first equation is negative, which should be made positive upon squaring.  When you take the square root of both sides, the negative is preserved, thus distorting the result.  Taking the square root of something squared, , is the same as taking the absolute value, .

Proof #4

This one is a bit tricky, especially if you don't remember complex and imaginary numbers.  The error in this theorem goes undetected because of the inculcation of a rule which is seldom taught with exceptions.  It lies in the seemingly harmless step in going from 2 to 3.

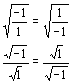
We are all taught that .  This is true when a and b are both positive.  With the possibility that a and b can be negative, and considering imaginaries, the rule is extended to .  Line 3 should actually read

If you still are not convinced, try cross-multiplying the original / erroneous line 3.  You get the untrue statement that -1 equals 1.  The negative correction above, also by cross multiplication yields -1 = -1.